FUNZIONI
Torniamo a parlare più attentamente delle funzioni. Le funzioni possono essere pensate come dei "programmi in miniatura" all'interno del programma principale, detti anche sottoprogrammi o subroutine, con cui potete organizzare e suddividere i programmi in parti piccole facilmente leggibili, testabili e riutilizzabili. Oltre alle numerose funzioni predefinite come input print int float, potete infatti creare facilmente le vostre funzioni personali.
Ecco come si definisce una funzione di base:def nome_funzione():
istruzione 1
...
istruzione n
Anche in questo caso l'indentazione serve per far capire al computer quali sono le istruzioni che formano il corpo della funzione. Per chiamare (attivare, avviare) questa funzione (cioè per eseguire le istruzioni in essa contenute) nel programma dovete scrivere:
nome_funzione()
a questo punto vengono eseguite le istruzioni interne alla funzione, poi il programma riprende l'esecuzione dall'istruzione successiva alla chiamata della funzione. Vediamo subito un esempio:
#------ PROGRAMMA CONVERSIONE PIEDI <--> METRI def metri_piedi(): m = float(input("METRI? ")) p = m / CONVERSIONE print(m, "METRI CORRISPONDONO A", p,"PIEDI") #--------------------------------------------------------------------- def piedi_metri(): p = float(input("PIEDI? ")) m = p * CONVERSIONE print(p, "PIEDI CORRISPONDONO A", m, "METRI") #--------------------------------------------------------------------- def stampa_menu(): print("----------------------------") print("1) CONVERTIRE METRI IN PIEDI") print("2) CONVERTIRE PIEDI IN METRI") print("3) FINE") print("----------------------------") #--------------------------------------------------------------------- def menu_principale(): while True: stampa_menu() sc = input("SCELTA: ") if sc == "1": metri_piedi() if sc == "2": piedi_metri() if sc == "3": break #--------------------------------------------------------------------- CONVERSIONE = 0.357 menu_principale() print("Goodbye")
Le funzioni vanno sempre scritte prima delle istruzioni del blocco principale del programma da cui vengono chiamate (il blocco principale si trova alla fine del listato). In questo esempio la prima riga di programma che viene eseguita è l'assegnazione di un valore alla variabile CONVERSIONE, poi viene chiamata la funzione menu_principale che contiene un ciclo senza fine (detto ciclo principale o main loop), il quale richiama la funzione stampa_menu (che si occupa di stampare le 5 righe che formano il menù), chiede all'utente quale scelta vuole effettuare, richiama le funzioni di conversione metri_piedi o piedi_metri a seconda che si sia scelto 1 o 2, oppure termina il ciclo in caso di scelta 3. Quando il ciclo principale termina viene stampata la stringa Goodbye. Se invece si immette una scelta non valida viene stampato di nuovo il menu, in sostanza si rimane nel loop principale finché non si effettua la scelta 3.
Il diagramma di flusso di un programma composto da funzioni prevede il simbolo rettangolo con due barre ai bordi che indicano la chiamata ad una funzione, e ogni funzione viene rappresentata da un piccolo diagramma a parte:
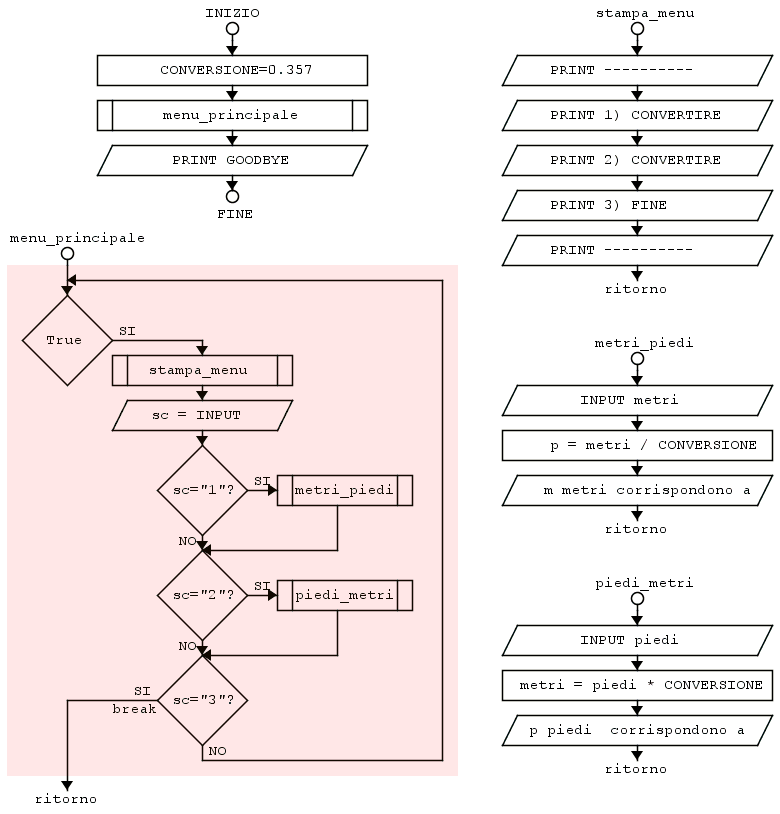
Come vedete le singole funzioni si possono immaginare racchiuse nei rettangoli di chiamata, questo è un aspetto molto importante perché permettono di nascondere i dettagli di una certa parte i codice dietro un semplice nome da "invocare" quando serve, a tutto vantaggio della chiarezza di lettura del programma e del minor numero di errori che si possono commettere. Inoltre una stessa funzione può essere chiamata più volte anche da punti diversi del programma, questo evita di riscrivere le stesse cose in due o più punti differenti. Un programma composto da molte piccole funzioni con nomi significativi coerenti con il loro scopo, e che svolgono un unico compito ben preciso, è stilisticamente un buon programma. Funzioni ben parametrizzate possono essere riutilizzate in altri programmi, il riutilizzo del codice evita di reinventare le stesse cose ogni volta.
ARGOMENTI
Al momento della chiamata di una funzione potete opzionalmente "passarle" dei dati (argomenti) scrivendoli ta parentesi. Nella definizione della funzione si specificano tra parentesi dei nomi (parametri) a cui vengono assegnati gli argomenti al momento della chiamata. Potete quindi immaginare i parametri come variabili in ingresso alla funzione, utilizzabili solo all'interno della funzione stessa:
def messaggio(msg):
print("IL MESSAGGIO E':", msg)
#---------------------------------------------------------------------
def stampa_prodotto(x, y):
print("IL PRODOTTO DI", x, "E", y, "VALE", x * y)
#---------------------------------------------------------------------
messaggio("QUESTO E' UN MESSAGGIO")
messaggio("E QUESTO E' UN ALTRO")
stampa_prodotto(10, 45)
VALORI DI RITORNO
Con return le funzioni possono opzionalmente "restituire" qualcosa alla riga chiamante (valore di ritorno) per essere usate in espressioni e assegnazioni, in questo caso si parla anche di "funzioni produttive", nel senso che producono un valore utilizzabile da chi le ha chiamate, in pratica in un'espressione contenente una funzione al posto della funzione viene considerato il valore prodotto in quel momento dalla funzione stessa:
def quadrato(a):
return a * a
#-------------------------------------------------------------------------
print(12 + quadrato(15))
z = quadrato(827.99)
USCITA ANTICIPATA DA UNA FUNZIONE
Potete anche usare return per uscire immediatamente dalla funzione da un punto qualsiasi delle istruzioni interne. Se return viene usato solo per uscire, senza ritornare un valore, non si parla più di funzione produttiva perché lo scopo di return in questo caso non è quello di restituire un valore al chiamante:
def stampa_quoziente(dividendo, divisore):
if divisore == 0:
print("IMPOSSIBILE DIVIDERE PER ZERO!")
return
print("QUOZIENTE =", dividendo / divisore)
#-------------------------------------------------------------------------
stampa_quoziente(100, 4)
stampa_quoziente(82, 0)
MODULI MATH E RANDOM
Python ha una enorme quantità di funzioni predefinite per i più disparati compiti. Le funzioni predefinite (built-in) sono sempre disponibili, altre sono contenute nei numerosi moduli di Python raccolte in categorie.
Ad esempio Il modulo matematico math, contiene tutte le funzioni trigonometriche e logaritmiche, per avere disponibili le funzioni di questo modulo basta scrivere all'inizio del programma:
import math
A questo punto è possibile richiamarle con math.nomefunzione(argomenti...)
print(math.sqrt(500)) # stampa la radice quadrata di 500
Ecco l'elenco delle funzioni matematiche avanzate che potrete usare per tracciare grafici, effettuare studi sulle funzioni e calcoli scientifici:
TRIGONOMETRICHE (gli angoli x sono espressi in radianti) math.sin(x) Seno di x math.cos(x) Coseno di x math.tan(x) Tangente di x math.asin(x) Arcoseno di x math.acos(x) Arcocoseno di x math.atan(x) Arcotangente di x math.hypot(x, y) Ipotenusa sqrt(x*x + y*y)
COSTANTI E CONVERSIONI ANGOLARI math.pi pigreco 3.1415926535897931 math.e base logaritmi naturali 2.7182818284590451 math.degrees(x) converte radianti in gradi (grad=rad*180/pi) math.radians(x) converte gradi in radianti (rad=grad*pi/180)
POTENZE E LOGARITMI math.exp(x) antilogaritmo naturale e**x math.log(x) logaritmo naturale in base e di x math.log(x, n) logaritmo in base n di x log(x)/log(n) math.log10(x) logaritmo in base 10 di x math.sqrt(x) radice quadrata di x
Un altro modulo interessante è random, che contiene una serie di funzioni per generare numeri casuali, utili nelle simulazioni o nei giochi.
import random print(random.randint(10, 30)) # numero casuale tra 10 e 30 (compresi)
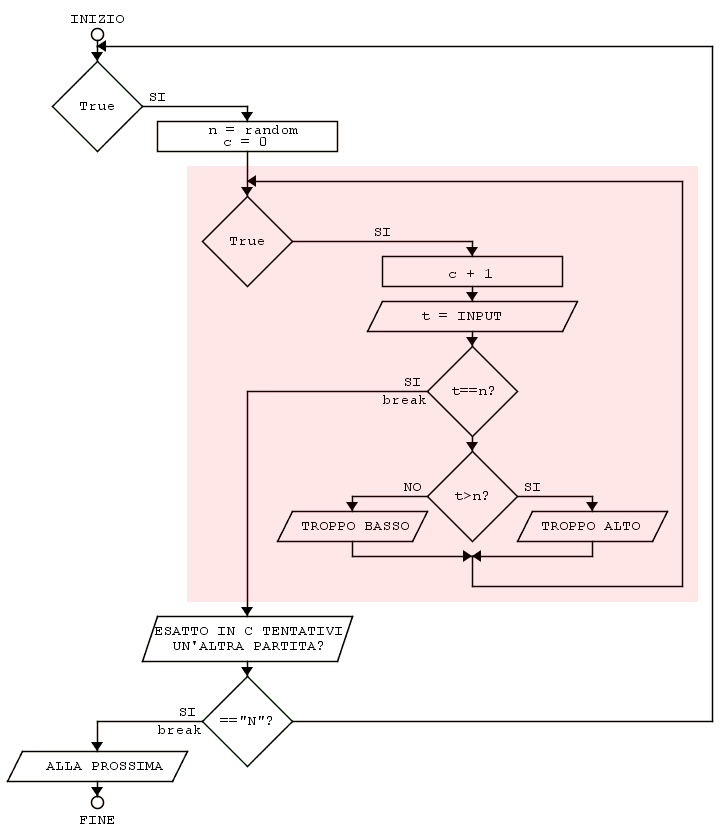
Con le nozioni acquisite fin qui dovreste essere in grado di comprendere abbastanza agevolmente il funzionamento del seguente programma. Se invece avete dei dubbi o alcune cose sono ancora incomprensibili, vi conviene tornare indietro, e ripassare attentamente i punti che ancora dovessero risultare oscuri tutte le volte che vi sarà necessario per chiarirli, anche se ci volessero settimane. Il consiglio è sempre quello di fare finta di essere voi stessi il computer e di seguire a mano le singole righe di programma cercando di capire cosa farebbe lui, aiutandovi magari con i diagrammi di flusso.
#------ PROGRAMMA INDOVINA IL NUMERO tra 1 e 1000 import random while True: n = random.randint(1, 1000) c = 0 while True: c = c + 1 t = int(input("TENTA: ")) if t == n: break if t > n: print("TROPPO ALTO") else: print("TROPPO BASSO") print("ESATTO!!! IN", c, "TENTATIVI.") if input("UN'ALTRA PARTITA (S/N)?") == "N": break print("ALLA PROSSIMA")
VISIBILITÀ
I nomi di variabile che usate nel programma non sono sempre visibili in ogni punto del programma stesso. In particolare in Python tutte le variabili che vengono assegnate all'interno di una funzione (compresi i parametri) sono "locali", esistono cioè solo all'interno della funzione e solo per il tempo della sua esecuzione. Quando la funzione termina, le variabili locali cessano di esistere.
Una variabile locale può anche avere lo stesso nome di una variabile già definita in un altro punto del programma, ma sono due variabili diverse che si riferiscono a dati differenti:
def f():
a = 30
print(a)
#-------------------------------------------------------------------------
a = "stringa"
print(a)
f()
print(a)
Risultato:
stringa 30 stringa
Invece "in lettura", cioè se non viene fatto un assegnamento all'interno della funzione, un nome esterno alla funzione è accessibile:
def f():
print(a)
#-------------------------------------------------------------------------
a = "stringa"
f()
Risultato:
stringa
Riassumendo: dall'interno di una funzione Python non è possibile assegnare qualcosa ad una variabile esterna alla funzione stessa (perché viene creata una variabile locale), ma è invece possibile "leggerla". Se serve assegnare qualcosa ad una variabile esterna alla funzione si può sfruttare il suo valore di ritorno:
def f(x):
return x + 1
#-------------------------------------------------------------------------
a = 100
print(a)
a = f(a)
print(a)
Risultato:
100 101
In genere però è bene che una funzione riceva tutti i dati su cui lavorare attraverso i parametri, e restituisca il risultato al chiamante tramite return. In questo modo la funzione è indipendente, cioè non è legata alla presenza di variabili esterne ad essa.
FUNZIONI NIDIFICATE
Potete anche definire delle funzioni all'interno di altre funzioni, in tal caso la funzione interna è locale a quella esterna, e può "vedere" tutte le variabili locali della funzione esterna (oltre a tutte le variabili del blocco principale del programma, dette "globali"), ma non le può comunque modificare.
def esterna():
def interna():
b = 20
print(a)
a = 120
print(a)
interna()
#-------------------------------------------------------------------------
esterna()
Risultato:
120 120
In questo esempio 'b' è una variabile locale della funzione interna, ed è visibile solo nella funzione interna stessa, mentre 'a' è una variabile locale della funzione esterna e può essere vista da entrambe le funzioni, ma non dal blocco principale del programma.
Allo stesso modo la funzione interna è una funzione locale di quella esterna, può essere chiamata solo dalla funzione esterna stessa, ma non dal blocco principale del programma.
In sostanza ciò che è più interno è nascosto a ciò che è più esterno, mentre ciò che è esterno è visibile anche nelle strutture interne (sempre se in esse non vengono fatti assegnamenti con gli stessi nomi usati all'esterno).
RICORSIONE
Un'immediata conseguenza dell'esistenza delle variabili locali è la possibilità per una funzione di chiamare una copia di sè stessa, questo tipo di chiamata viene detta ricorsiva.
Ad ogni chiamata ricorsiva, le variabili interne della nuova copia della funzione sono variabili locali nuove e indipendenti. Chiamare sè stessa non è diverso dal chiamare un'altra funzione. Se una funzione chiama sè stessa, e la copia chiama un'altra volta sè stessa, si è esattamente nella stessa situazione di una funzione 'a' che chiama una funzione 'b che chiama una funzione 'c'. Quando 'c' termina, riprende l'esecuzione di 'b', e quando anche 'b' termina, riprende l'esecuzione di 'a'. Una funzione ricorsiva può chiamare sè stessa innumerevoli volte (idealmente anche infinite) creando una catena di funzioni "in sospeso", fino al momento in cui l'ultima chiamata ritorna, poi la penultima ritorna e così via fino alla prima.
Per questo motivo, cioè il poter produrre una lunga catena di funzioni "aperte" ciascuna con le proprie variabili locali, la ricorsione può occupare molta memoria del computer, e in Python in particolare il numero di copie di una funzione è limitato a circa 900.
La ricorsione risulta abbastanza "scomoda" da seguire mentalmente, tuttavia ci sono alcuni problemi che hanno una natura intrinsecamente ricorsiva, o che comunque possono essere descritti in modo ricorsivo. Ad esempio pensiamo alla somma di tutti i numeri compresi tra 0 ed n. Si può certamente scrivere un programma che la calcola in modo non ricorsivo:
n = int(input("Immettere un numero: ")) totale = 0 while n > 0: totale = totale + n n = n - 1 print(totale)Ma si può anche pensare al risultato in termini ricorsivi:
somma = n + somma(n-1)
cioè il totale vale mio numero più la somma di tutti i precedenti, la somma dei precedenti segue la stessa logica con n diminuito di uno e così via. Fino a un caso limite che interrompe il processo, in questo caso quando n vale 0 non ha più senso continuare con la "somma dei precedenti". Il programma scritto in modo ricorsivo è il seguente:
def somma(n):
if n == 0:
return 0
else:
return n + somma(n-1)
#-------------------------------------------------------------------------
n = int(input("Immettere un numero: "))
totale = somma(n)
print(totale)
È importante inserire sempre la condizione di terminazione della ricorsione, in questo caso una chiamata alla funzione con argomento 0 le fa ritornare direttamente il valore 0 senza chiamare di nuovo sè stessa.
La difficoltà iniziale a comprendere il funzionamento di una funzione ricorsiva è spesso dovuta al fatto di pensare alle chiamate ricorsive come ad un ciclo che usa sempre le stesse variabili, e perciò non è chiaro né il flusso dell'esecuzione, né "dove" si trovino o si accumulino i risultati intermedi.
In realtà nella ricorsione non vi è alcun ciclo, ma solo una lunga catena di funzioni chiamate una dentro l'altra (ciascuna con le sue variabili "personali", ecco dove sono i valori intermedi!). Ad esempio un gruppo di funzioni che simula il flusso della precedente funzione somma per valori di n compresi tra 0 e 3 può essere il seguente:
def somma(n): # da chiamare con n da 0 a 3 if n == 0: return 0 else: return n + somma_b(n-1) def somma_b(n): if n == 0: return 0 else: return n + somma_c(n-1) def somma_c(n): if n == 0: return 0 else: return n + somma_d(n-1) def somma_d(n): if n == 0: return 0 else: # questo caso non e` gestibile #------------------------------------------------------------------------- print(somma(3))